AI advocates have expressed frustration at Ted Chiang’s critique of AI in The New Yorker, where he argued that large language models “take an average of the choices that other writers have made.” Yes it’s a simplification, but it’s also correct at a fundamental level.
Chiang’s criteria for artistic quality—eg, the number of choices made by the artist, and by extension, the amount of labor involved—strike me as naive, especially for visual art. But he’s right that LLMs are averaging machines, and this insight helps explain their power and limitations.
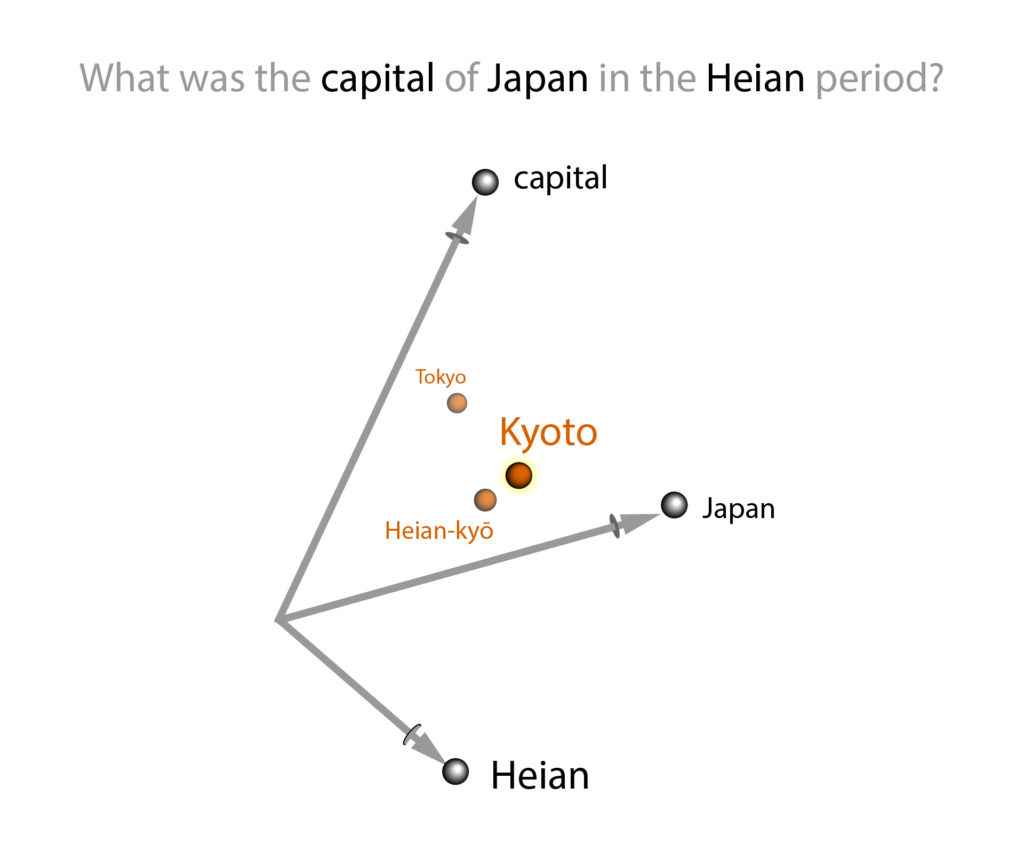
Training an LLM starts by scraping billions of pages from the web and designing a mathematical space where every word corresponds to a different point. Engineers then write software that picks a pair of words (like “capital” and “Japan”) and checks how often they appear next to each other in these documents. The engineers then systematically move points around in this space until words that cluster semantically in human texts also cluster spatially in this mathematical space.
When you type “What was the capital of Japan in the Heian period?” into a model trained in this way, the model effectively finds the word closest to the average position of the query terms. With enough sentences like “Kyoto was Japan’s capital in the Heian period” in the training data, the word Kyoto should appear near the midpoint of the points corresponding to Japan, capital, and Heian.
Technically the model chooses its answer via a weighted vector sum because the context implies some words are more important than others; here the word “Heian” is obviously important than the word “the.” But guess what: a weighted vector sum is mathematically equivalent to an average.
To be sure, any large language model with a temperature set higher than zero will gather a number of possible answers near the query average. If there is a clear winner, it typically returns that: the capital of Heian Japan was Kyoto. When there’s no answer right at the midpoint, the LLM will roll dice to choose among the nearest neighbors. This can result in a different but equally correct answer (like Heian-kyō), or with a high-enough temperature, a completely incorrect answer (like Tokyo or Seoul).
Of course, neural networks do employ math that isn’t averaging—particularly in training and fine-tuning, where engineers apply techniques like cosine similarities and gradient descent. However, to claim therefore that large language models don’t produce results by averaging is like saying internal combustion cars don’t run on gas because they have batteries or were manufactured in a solar-powered factory.
AI companies would like us to view generative AI as a pinnacle of software development whose complexity could give rise to emergent intelligence or even consciousness. But we call LLMs “black boxes” not because they are intricate like circuit diagrams from the future but because they are messy like bowls of tangled spaghetti. Training them means brute-forcing billions of comparisons, and running them means averaging the results of their training.
Understanding its averaging dynamic helps makes sense of generative AI’s frequently mediocre or stereotypical results, which Chiang points to in his article. (Averages can also mislead: see the midpoint hottie problem.) Averaging furthermore explains why an absence of good data points in the vicinity of the mathematical average can yield nonsensical results, like Google telling you to glue cheese to a pizza.
On the positive side, realizing how simple large language models are can make their versatility all the more impressive. I find it mind-boggling that repeating such a dumb process a ridiculous number of times ends up generating tactful emails, functioning HTML games, and romantic comedies based on the periodic table. For these examples, the result of averaging can seem well above average.